Тригонометрия срочно

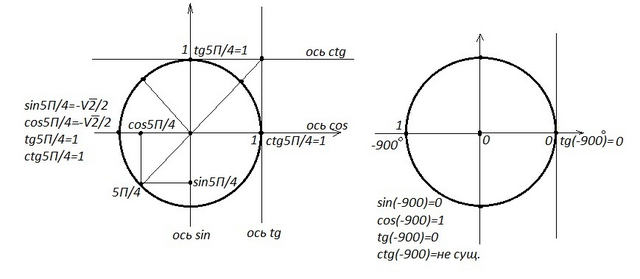
0\; ,\\\\sin\beta =\sqrt{1-cos^2\beta }=\sqrt{1-\frac{1}{4}}=\frac{\sqrt3}{2}" alt="1)\; \; sin\frac{5\pi }{4}=cos\frac{5\pi }{4}=-\frac{\sqrt2}{2}\; \; ,\; \; tg\frac{5\pi }{4}=ctg\frac{5\pi }{4}=1\\\\sin(-900^\circ)=0\; ,\; \; cos(-900^\circ )=-1\; ,\; \; tg(-900^\circ )=0\; ,\\ctg(-900^\circ )\; -\; ne\; syshestvyet\\\\2)\; \; cosa=-\frac{\sqrt2}{2}\; \; ,\; \; a\in (\pi ,\frac{3\pi}{2})\; \to \; sina<0\; ,\\\\sina=-\sqrt{1-cos^2a}=-\sqrt{1-\frac{2}{4}}=-\frac{\sqrt2}{2}\\\\cos\beta=\frac{1}{2}\; \; ,\; \; \beta \in (0,\frac{\pi}{2})\; \to \; sin\beta >0\; ,\\\\sin\beta =\sqrt{1-cos^2\beta }=\sqrt{1-\frac{1}{4}}=\frac{\sqrt3}{2}" align="absmiddle" class="latex-formula">

$cos(a+\beta )=cosa\cdot cos\beta -sina\cdot sin\beta =-\frac{\sqrt2}{2}\cdot \frac{1}{2}+\frac{\sqrt2}{2}\cdot \frac{\sqrt3}{2}=\frac{\sqrt6-\sqrt2}{4}\\\\3)\; a)\; 1-2sin^2\frac{\pi}{8}=cos(2\cdot \frac{\pi}{8})=cos\frac{\pi}{4}=\frac{\sqrt2}{2}\\\\b)\; \; sin105^\circ =sin(60^\circ +45^\circ )=sin60^\circ \cdot cos45^\circ +cos60^\circ \cdot sin45^\circ =\\\\=\frac{\sqrt3}{2}\cdot \frac{\sqrt2}{2}+\frac{1}{2}\cdot \frac{\sqrt2}{2}=\frac{\sqrt6+\sqrt2}{4}\\\\c)\; \; ctg\frac{7\pi}{4}=ctg(2\pi -\frac{\pi }{4}=ctg(-\frac{\pi}{4})=-ctg\frac{\pi}{4}=-\frac{\sqrt2}{2}$

$4)\; \; cos^4a+sin^4a-2cos^2a\, sin^2a=(cos^2a-sin^2a)^2=(cos2a)^2=cos^22a\; ;\\\\(1-cos^2a)\cdot ctga=sin^2a\cdot \frac{cosa}{sina}=sina\cdot cosa$