В равнобедренной трапеции ABCD основания AD и BC равны 10 см и 2 см соответственно, а...

Question

В равнобедренной трапеции ABCD основания AD и BC равны 10 см и 2 см соответственно, а боковые стороны AB=CD=5. Биссектриса угла BAD пересекает продолжение основания BC в точке E. Найдите квадрат биссектрисы угла ABE в треугольнике ABE. Это срочно, помогите пожалуйста

Answer 1

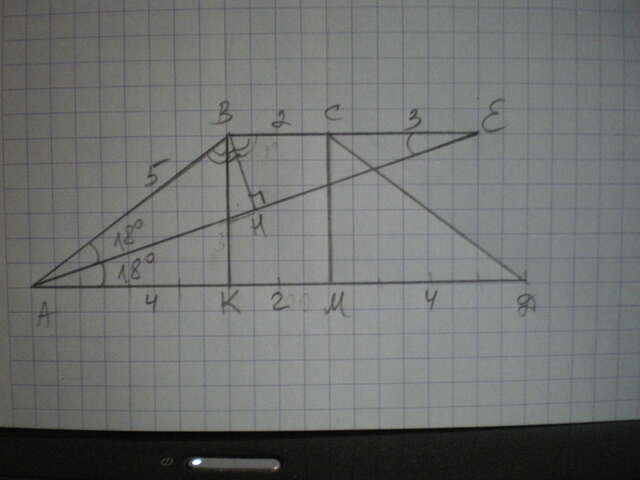
Рассмотрим ΔАВЕ - равнобедренный, т.к. ∠ВАЕ=∠ДАЕ по условию, ∠АЕВ=∠ЕАД как внутренние накрест лежащие при АД║ВЕ.

Таким образом ВН - не только биссектриса, но и высота ΔАВЕ.

Проведем высоты ВК и СМ. КМ=ВС=2 см, АК=МД=(10-2):2=4 см.

Рассмотрим ΔАВН - прямоугольный. Косинус ∠ВАК=АК\АВ=4\5=0,8. Значит, ∠ВАК=36°.

Тогда ∠ВАН=36:2=18°.

По теореме синусов ВН=АВ*sin18°=5*0,309=1,545 см.

Квадрат этой величины составляет 1,545²=2,387.

В ответ запишем 2,4.

---