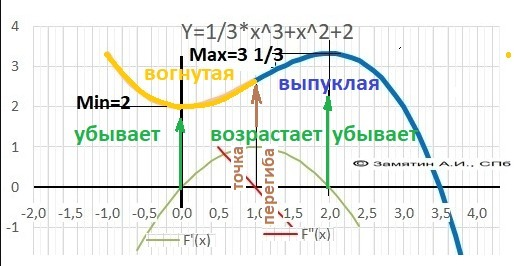
ДАНО: Y(x) = - 1/3x³ + x² + 2.
ИССЛЕДОВАНИЕ
1.Область определения D(x) - Х∈(-∞;+∞) - непрерывная, гладкая. Нет причин для разрывов - деления на ноль.
2. Пересечение с осью Х - нуль функции. Y=0 при X₁ ≈ 3.5
Положительна - X∈(-∞;X₁), отрицательна - X∈(X₁;+∞).
3. Пересечение с осью У. У(0) = 2.
4. Поведение на бесконечности.limY(-∞) = + ∞ limY(+∞) = -∞
5. Исследование на чётность.
Ответ силой Разума: если все степени при Х - чётные, то и функция - чётная, если все степени нечетные - функция нечётные. Смотрим и видим, что в нашей функции и третья степени при Х и вторая. Вывод - ни то, ни сё.
Y(-x) = 1/3*x³ + x² + 2 ≠ - Y(x) ≠ Y(x).
Функция ни чётная ни нечётная.
6. Производная функции.Y'(x)= -x² +2*х = -x*(x -2).
Корни при Х₂= 0 и Х₃ = 2. Схема знаков производной.
(-∞)__(<0)__(0)___(>0)___(2)__(<0)_____(+∞)</p>
7. Локальные экстремумы.
Максимум Ymax(2)= 10/3 = 3 1/3, минимум – Ymin(0)=2.
8. Интервалы возрастания и убывания.
Возрастает - Х∈[0;2], убывает = Х∈(-∞;0]∪[2;+∞).
9. Вторая производная - Y"(x) = -2*x +2 = -2*(x-1) =0.
Корень производной - точка перегиба - при х= 1.
10. Выпуклая “горка" Х∈[1;+∞), Вогнутая – "ложка" Х∈(-∞;].
11. График в приложении.