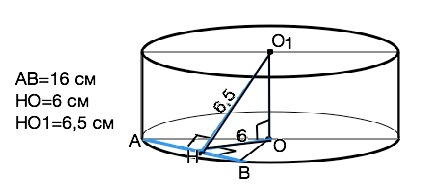
Расстояние между прямой и точкой равно длине отрезка, проведенного перпендикулярно между ними На рисунке приложения ОО1 - расстояние между центрами оснований цилиндра и равно его высоте. АВ - данная по условию хорда. НО - расстояние от хорды до центра нижнего основания, НО1 - расстояние от нее до центра верхнего основания. АО=ВО=R; ОН⊥АВ; О1Н⊥АВ
Площадь полной поверхности цилиндра равна сумме площадей двух оснований и боковой поверхности. S(полн)=2•Ѕ(осн)+Ѕ(бок)
S(полн)=2•πR²+2πR•H
Из прямоугольного треугольника АОН по т.Пифагора R²=AH²+OH²=(16:2)²+6²=100 см² ⇒ R=10 см; из прямоугольного треугольника ОО1Н высоту найдем по т.Пифагора H=OO1=√(O1H²-OH²)= √(6.5²-6²)=2,5 см
S(полн)=π•200+2π•10•2,5=250π см²