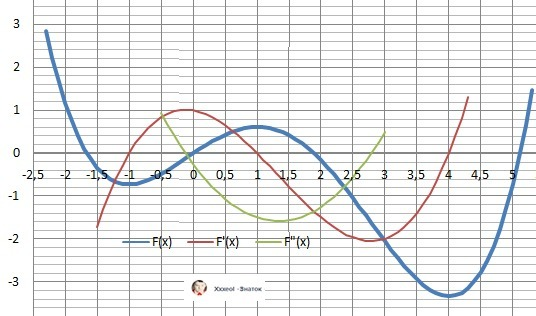
ДАНО: y(x) = 1/16*x⁴ - 1/3*x³ - 1/8*x² + x
ИССЛЕДОВАНИЕ на экстремумы. Функция непрерывная.
Экстремумы находятся в корнях первой производной.
y'(x) = 1/4*x³ - x² - 1/4*x + 1 = 1/4*x*(x²-1) - (x²-1) = (x-1)*(x+1)(x-4) = 0 .Корни: x₁ = - 1 , x₂ = 1, x₃ = 4 - точки экстремумов.
Интервалы монотонности: парабола четвертого порядка
Убывает - Х∈(-∞;-1]∪[1;4]
Минимум - Ymin(-1) = 1/16 + 1/3 - 1/8 - 1 = - 35/48 (≈ - 0.73)
Возрастает - X∈[-1;1]∪[4;+∞]
Максимум - Ymax(1) = 1/16 - 1/3 - 1/8 + 1 = 29/48 (≈0.60)
Минимум - Ymin(4) = = 256/16 - 64/3 - 16/8 + 4 = - 3 1/3 (≈ - 3.33)
График функции и её производных на рисунке в приложении.