Помогите с геометрией очень прошу !!!Я никак не пойму как решить задачку ** Укр. в...

Question

Помогите с геометрией очень прошу !!!Я никак не пойму как решить задачку На Укр. в трапеції abcd ad=5 bc=4 ТОЧКА E ділить сторону ab у відношенні AE:EB 3:1 Через точку E паралельно до основ проведена пряма що перетинає сторону cd у точці F обчислити довжину EF На Рус. в трапеции abcd ad = 5 bc = 4 ТОЧКА E делит сторону ab в отношении AE: EB 3: 1 Через точку E параллельно к основаниям проведена прямая что пересекает сторону cd в точке F вычислить длину EF

Answer 1

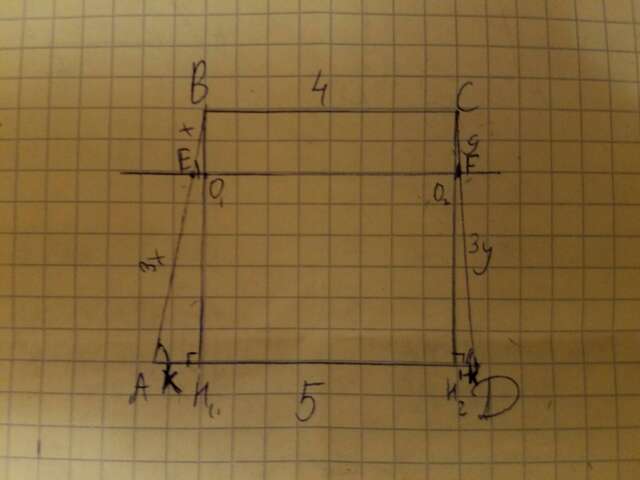
BC || EF || AD, AE : EB = 3 : 1, значит, по теореме Фалеса DF : FC = 3 : 1.
Опустим высоты BH1 и CH2. H1H2 = BC = O1O2 = 4, так как BCH2H1, BCO2O1 — прямоугольники. Пусть AH1 = k, тогда H2D = AD - AH1 - H1H2 = 1 - k.
Рассмотрим треугольники AH1B и EO1B: углы H1 и O1, A и E равны как соответственные — треугольники подобны по I признаку. Коэффициент подобия равен 1 : (1 + 3) = 1 : 4. Тогда EO1 = k / 4. Аналогично рассуждая, получим O2F = (1 - k) / 4.
EF = EO1 + O1O2 + O2F = k / 4 + 4 + (1 - k) / 4 = (k + 1 - k) / 4 + 4 = 1 / 4 + 4 = 4,25.

Ответ: 4,25

---

Answer 2

Проводим среднюю линию трапеции абсд и обозначаем ее мн. Она равна 4,5. Затем рссматриваем трапецию мбсн, в ней отрезок еф будет средней линией и поэтому еф равна 4,25.