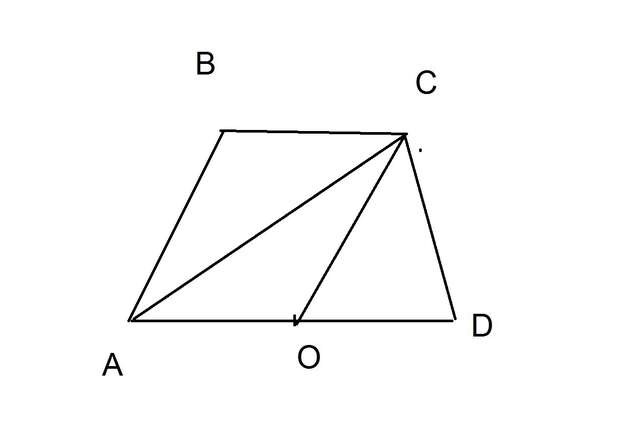
пусть точка О - середина основания AD
проведем отрезок СО
так как BC в два раза меньше AD то АО=BC
так как ABCD - трапеция то AD║BC
Теорема. если в четырехугольнике две стороны равны и параллельны то этот четырехугольник параллелограмм
⇒ABCO - параллелограмм
в параллелограмме противоположные стороны равны ⇒СО=АВ
а так как BC=AB то СО=BC и АО=ОС=ОД ⇒ О - центр описанной около треугольника АСD окружности.
Если центр описанной окружности лежит на стороне треугольника то такой треугольник прямоугольный и сторона является гипотенузой.
⇒АСD - прямоугольный треугольник с гипотенузой AD ⇒ ∠ACD прямой. ∠ACD=90°