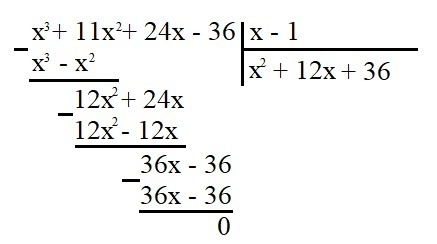Пусть ![\sqrt[3]{x}=a, \sqrt[3]{2x+6}=b, \sqrt[3]{3x+24}=c](https://tex.z-dn.net/?f=%5Csqrt%5B3%5D%7Bx%7D%3Da%2C%20%5Csqrt%5B3%5D%7B2x%2B6%7D%3Db%2C%20%5Csqrt%5B3%5D%7B3x%2B24%7D%3Dc "\sqrt[3]{x}=a, \sqrt[3]{2x+6}=b, \sqrt[3]{3x+24}=c")
. Тогда
Заменим a + b на c:
![3abc=c^3-a^3-b^3\\3\sqrt[3]{x(2x+6)(3x+24)}=3x+24-x-2x-6\\ 3\sqrt[3]{6x(x+3)(x+8)}=18\\ \sqrt[3]{6x(x+3)(x+8)}=6\\ 6x(x+3)(x+8)=216\\ x(x+3)(x+8)=36\\ x^3+11x^2+24x-36=0](https://tex.z-dn.net/?f=3abc%3Dc%5E3-a%5E3-b%5E3%5C%5C3%5Csqrt%5B3%5D%7Bx%282x%2B6%29%283x%2B24%29%7D%3D3x%2B24-x-2x-6%5C%5C%203%5Csqrt%5B3%5D%7B6x%28x%2B3%29%28x%2B8%29%7D%3D18%5C%5C%20%5Csqrt%5B3%5D%7B6x%28x%2B3%29%28x%2B8%29%7D%3D6%5C%5C%206x%28x%2B3%29%28x%2B8%29%3D216%5C%5C%20x%28x%2B3%29%28x%2B8%29%3D36%5C%5C%20x%5E3%2B11x%5E2%2B24x-36%3D0 "3abc=c^3-a^3-b^3\\3\sqrt[3]{x(2x+6)(3x+24)}=3x+24-x-2x-6\\ 3\sqrt[3]{6x(x+3)(x+8)}=18\\ \sqrt[3]{6x(x+3)(x+8)}=6\\ 6x(x+3)(x+8)=216\\ x(x+3)(x+8)=36\\ x^3+11x^2+24x-36=0")
Заметим, что x = 1 - корень уравнения. Тогда разделим 
на 
(см. картинку). Получим 
. Тогда уравнение будет иметь вид:
Так как производилась замена a + b на c, могли появиться посторонние корни. Сделаем проверку:
x = -6:
![\sqrt[3]{-6}+\sqrt[3]{2*(-6)+6}=\sqrt[3]{3*(-6)+24}\\ \sqrt[3]{-6}+\sqrt[3]{-6}=\sqrt[3]{6}\\-2\sqrt[3]{6}=\sqrt[3]{6}](https://tex.z-dn.net/?f=%5Csqrt%5B3%5D%7B-6%7D%2B%5Csqrt%5B3%5D%7B2%2A%28-6%29%2B6%7D%3D%5Csqrt%5B3%5D%7B3%2A%28-6%29%2B24%7D%5C%5C%20%5Csqrt%5B3%5D%7B-6%7D%2B%5Csqrt%5B3%5D%7B-6%7D%3D%5Csqrt%5B3%5D%7B6%7D%5C%5C-2%5Csqrt%5B3%5D%7B6%7D%3D%5Csqrt%5B3%5D%7B6%7D "\sqrt[3]{-6}+\sqrt[3]{2*(-6)+6}=\sqrt[3]{3*(-6)+24}\\ \sqrt[3]{-6}+\sqrt[3]{-6}=\sqrt[3]{6}\\-2\sqrt[3]{6}=\sqrt[3]{6}")
Равенство не выполнилось - корень не подходит.
x = 1:
![\sqrt[3]{1}+\sqrt[3]{2+6}=\sqrt[3]{3+24}\\\sqrt[3]{1}+\sqrt[3]{8}=\sqrt[3]{27}\\1+2=3\\3=3](https://tex.z-dn.net/?f=%5Csqrt%5B3%5D%7B1%7D%2B%5Csqrt%5B3%5D%7B2%2B6%7D%3D%5Csqrt%5B3%5D%7B3%2B24%7D%5C%5C%5Csqrt%5B3%5D%7B1%7D%2B%5Csqrt%5B3%5D%7B8%7D%3D%5Csqrt%5B3%5D%7B27%7D%5C%5C1%2B2%3D3%5C%5C3%3D3 "\sqrt[3]{1}+\sqrt[3]{2+6}=\sqrt[3]{3+24}\\\sqrt[3]{1}+\sqrt[3]{8}=\sqrt[3]{27}\\1+2=3\\3=3")
Равенство выполнилось - корень подходит.
Ответ: 1
