Ответ:
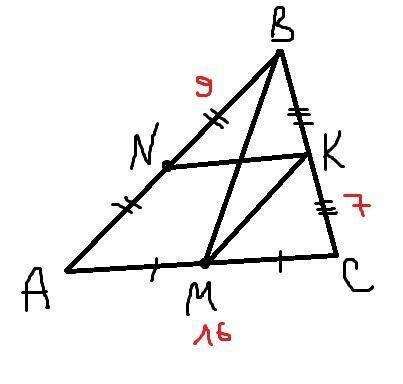
ВМ - медиана, значит М-середина АС.
М-середина АС, МК параллелен АВ, значит К-середина ВС.
К-середина ВС, KN параллелен AC, значит N-середина АВ.
N-середина АВ, значит АN=NВ=9.
КС=7, АС=16 -по условию.
К-середина ВС, N-середина АВ, значит NК-средняя линия и NК=АС:2=16:2=8.
Р=9+8+7+16=40.