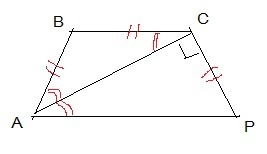
∠ВАС=∠ВСА, так как по условию ВС=АВ. ∠ВСА=∠САР как накрест лежащие при параллельных ВС и АР, и секущей АС, значит ∠ВАС=∠САР. ∠А=∠ВАС+∠САР. ∠В=∠ВСА+∠АСР. По условию ∠АСР=90°.
Существует свойство равнобокой трапеции: сумма противоположных углов в равнобокой трапеции равна 180°. Значит ∠А+∠С=180°. Подставим значения этих углов: ∠ВАС+∠САР+∠ВСА+90=180°.⇒ 3∠ВСА=90°⇒∠ВСА=30°⇒∠А=∠ВАС+∠САР=30+30=60°, ∠Р=∠А=60°.
В трапеции сумма углов, прилежащих к одной стороне равна 180°.⇒ ∠В=∠С=120°