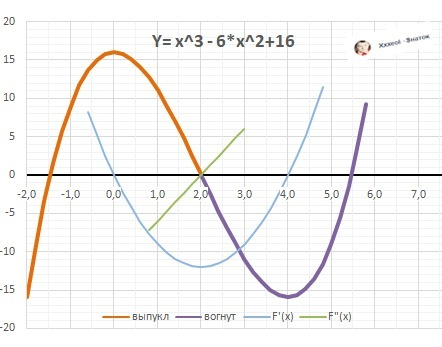
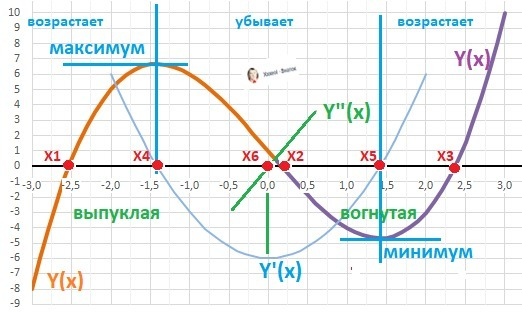
ДАНО: Y = x³ - 6*x² + 16
ИССЛЕДОВАНИЕ.
1. Область определения D(у) - Х∈(-∞;+∞) - непрерывная, гладкая.
2. Пересечение с осью ОХ - поиск нулей функции.
Применим метод неопределённых коэффициентов:
Y(х) = (x-x₁)*(x-x₂)*(x-x₃) = 0. Вспомним теорему Безу:
свободный член уравнения (+16) является произведением всех трёх корней: х₁*х₂*х₃ = 16. Например, 16 = 2*8. Возможно х₂= 2 корень. Делим многочлен Y(x) на (х-2) - "в столбик". Расчет приведен на рисунке в приложении. Остатка при делении нет - значение х = 2 - один из нулей функции. Первый этап разложения: Y(х)= x³-6*x²+16 = (x-2)*(x²-4*x-8)
Два других нуля функции получаем решением уравнения:
y = x² - 4*x - 8 = 0. Дискриминант D= 48 >0 - есть два корня. √D=√48 = √(16*3) = 4√3. х₁=2-2√3 (≈-1,46) и х₃=2+2√3 (≈5,46).
В итоге Y= x³-6*x²+16 = (x- 2-2√3)*(x-2)*(x-2+2√3) - разложили на множители. Получили три нуля функции:
х₁=2-2√3, х₂ = 2, х₃=2+2√3
3. Поведение на бесконечности.
(-x)³ = - x³ и limY(-∞)= - ∞ limY(+∞) = +∞
ВАЖНО: На бесконечности влияет только первый член уравнения, остальными можно пренебречь.
4. Интервалы знакопостоянства.
Y(x)<0 - X∈(-∞;Х₁)∪(Х₂;Х₃) <em>- от -∞ до первого нуля и между вторым и третьим нулями функции.
Y(x)>0 - X∈(Х₁;Х₂)∪(Х₃;+∞) - между первым и вторым нулём функции и далее от третьего нуля функции до +∞.
5 Пересечение с осью ОУ.
У(0) = 16 - свободный член уравнения.
6. Исследование на чётность.
ВАЖНО: У чётных функции - только чётные степени при Х, у нечётных - только нечётные.
Y(-x) = - x³- 6*x² +16 ≠ Y(x). Y(-x) ≠ -Y(x), - есть х² - чётная степень .
Функция ни чётная ни нечётная.
7. Производная функции.Y'(x)= 3*x² - 12*Х = 3*x*(x-4) = 0.
Корни первой производной: х₄= 0, х₅ = 4
8. Локальные экстремумы - в корнях первой производной.
Максимум Ymax(Х₄=0)= 16 , минимум – Ymin(Х₅=4) = - 16.
9. Интервалы монотонности.
Схема знаков производной - отрицательная между корнями.. (-∞)__(>0)__(Х₄)___(<0)___(Х₅)</strong>__(>0)_____(+∞)
ВАЖНО: Функция возрастает - когда производная Y'(x)>0, и убывает, когда производная Y'(x)<0 - между её корнями.</em>
Возрастает: Х∈(-∞;Х₄]∪[Х₅;+∞), убывает: Х∈[Х₄; Х₅].
ВАЖНО: нет разрывов у функции - квадратные скобки рядом с корнями.
10. Вторая производная: Y"(x) = 6*x-12 = 6*(х-2)=0.
Корень производной - точка перегиба Х₆= 2.
11. Интервалы выпуклости и вогнутости.
ВАЖНО: Вторая производная Y"(x)<0 - функция выпуклая ("горка"), Y"(x)>0 - вогнутая ("ложка"). Точка перегиба находится посередине между экстремумами.
Выпуклая: Х∈(-∞; Х₆=2]. Вогнутая: Х∈[Х₆=2; +∞).
12. Асимптоты функции.
ВАЖНО: Асимптот - нет, ни вертикальных, ни горизонтальных, ни наклонных.
13. Область значений. E(y) = R = (-∞;+∞) - следует из п. 3.
14. Рисунки к задаче с графиками в приложении.