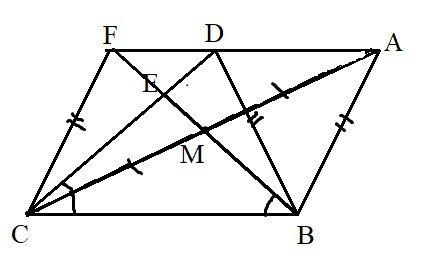
Проведём CF || AB, F ∈ AD. AF || BC, т. к. AD || BC как основания трапеции, CF || AB по построению ⇒ ABCF - параллелограмм ⇒ AB = CF. Но AB = BD по условию, значит, BD = CF ⇒ BDFC - равнобедренная трапеция.
Так как M - середина диагонали AC параллелограмма ABCF ⇒ M ∈ BF. Тогда BF и CD - диагонали равнобедренной трапеции. Они образуют с основаниями равные углы, отсюда треугольник BEC - равнобедренный ⇒ BE = CE, что и требовалось доказать.