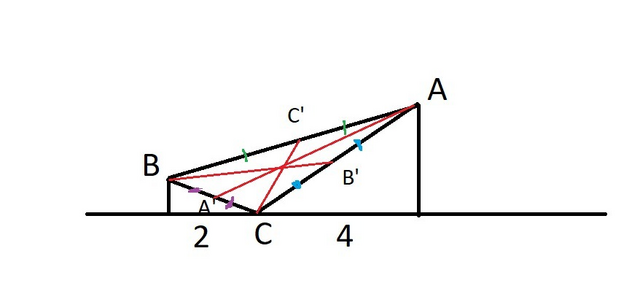
Смотрите чертёж (красные линии - медианы).
Считаем, что проекция AC равна 4, а проекция BC равна 2.
Проекции BA' и CA' равны (и равны 1, так как проекция BC равна 2). То же самое можно сказать и про проекции CB' и AB', но они равны 2. Так как треугольник тупоугольный, а AB лежит против тупого угла, проекция AB равна 6, а проекции AC' и BC' равны 3. Значит, проекция BB' равна сумме проекций BC и CB' (4), проекция AA' равна сумме проекций AC и CA' (5), а проекция CC' равна разности проекций BC и BC' (1). Значит, сумма проекций медиан данного треугольника - 10.
Ответ: 10.