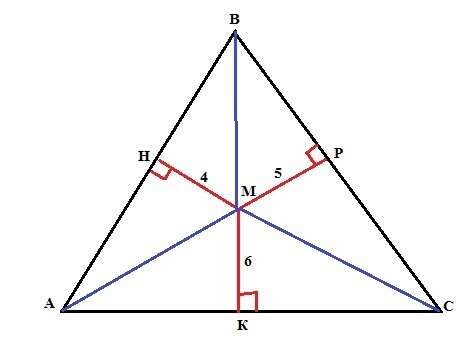
Пусть дан правильный треугольник АВС со стороной "а". Тода его площадь равна S=(√3/4)*a² (формула). Пусть дана точка М внутри треугольника таая, что МН=4см, МР=5см и МК=6см, где МН, МР и МК - перпендикуляры к сторонам АВ, ВС и АС соответственно или, что одно и то же, высоты треугольников АМВ,ВМС и АМС соответственно. Площадь треугольника АВС равна сумме площадей этих треугольников, то есть (1/2)*4*а+(1/2)*5*а+(1/2)*6*а = (√3/4)*а² => а = 7,5*4/√3.
Итак, сторона нашего треугольника равна 10√3. Тогда по приведенной выше формуле Sabc = (√3/4)*300 = 75√3 см².
Ответ: Sabc= 75√3 см².