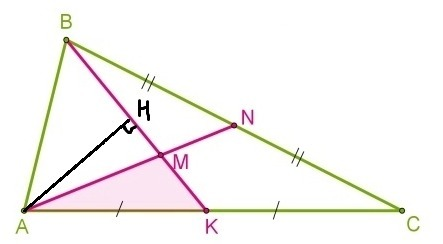
Проведём высоту AH к BK. Для треугольников ABM и AMK она общая, значит, их площади относятся как основания. BM : MK = 2 : 1, так как M - точка пересечения медиан. Тогда S(ABM) : 10 = 2 : 1 ⇒ S(ABM) = 20 см² ⇒ S(ABK) = S(ABM) + S(AMK) = 20 + 10 = 30 см².
Медиана BK делит треугольник ABC на два равновеликих ⇒ S(ABK) = S(BKC) ⇒ S(ABC) = 2S(ABK) = 2 * 30 = 60 см².
Ответ: 60