Начертить график y=5/x^2 - 1 через план производной

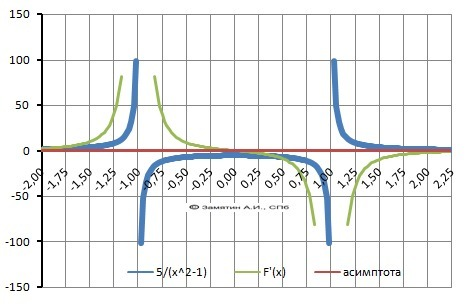
Ответ: Рисунок с графиком функции в приложении.

ДАНО: Y(x) = 5/(x²-1).

Пошаговое объяснение:

1. Область определения. (x²-1) = (x-1)*(x+1) ≠ 0. x ≠ +/- 1 - разрывы.

D(y) = (-∞;-1)∪(-1;1)∪(1;+∞)

2. Вертикальные асимптоты: Y = -1, Y = 1.

3. Пересечение с осью Х - Y(x) = 0 - нет.

4. Пересечение с осью Y - Y(0) = -5.

5. Поведение в точках разрыва.

lim(-1-) = +∞, lim(-1+) = -∞, lim(1-) = -∞, lim(1-) = +∞,

Горизонтальная асимптота: Y = 0.

6. Интервалы знакопостоянства.

Положительна: X∈(-∞;-1)∪(1;+∞), отрицательна: X∈(-1;1)

7. Проверка на чётность.

Y(-x) = Y(x) - функция чётная.

8. Поиск экстремумов - корни первой производной.

$Y'(x)=-\frac{10x}{(x^2-1)^2}=0\\$ - корень Х = 0.

9. Локальный экстремум. Максимум Y(0) = -5.

10. Интервалы монотонности.

Возрастает: X∈(-∞;-1)∪(-1;0), убывает: X∈(0;1)∪(1;+∞)

11. Поиск перегибов - корни второй производной.

$Y"(x)=-\frac{2}{(x^2-1)^2}+\frac{40x^2}{(x^2-1)^3}=0$ - корней нет.

12. Выпуклая - "горка" - X∈(-1;1); вогнутая - "ложка" - X∈(-∞;-1)∪(1;+∞).

13. График на рисунке в приложении.