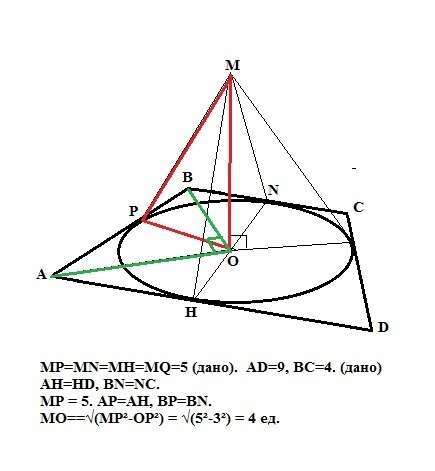
Пусть дана равнобедренная трапеция АВСD. Из условия ясно, что точка М проецируется в центр О вписанной в трапецию окружности, так как расстояние от точки М до стороны - это перпендикуляр из точки М к стороне, а радиус вписанной окружности - перпендикуляр из точки О на плоскости трапеции к ее стороне. Основания этих перпендикуляров находятся в одной точке по теореме о трех перпендикулярах. Диаметр вписанной в нашу трапецию окружности пройдет через середины ее оснований, значит боковая сторона трапеции будет равна сумме двух отрезков: половин большего и меньшего оснований, так как касательные из одной точки к окружности равны, то АР=АН и ВР=ВN (см. рисунок). Но ОР - это высота из прямого угла треугольника АОВ (боковая сторона видна под углом 90° из центра вписанной окружности - свойство). и по ее свойству равна ОР = √(АР*ВР) = √(2*4,5) = 3 ед. Тогда по Пифагору из прямоугольного треугольника МОР найдем искомое расстояние МО.
МО=√(МР²-ОР²) = √(5²-3²) = 4 ед. Это ответ.