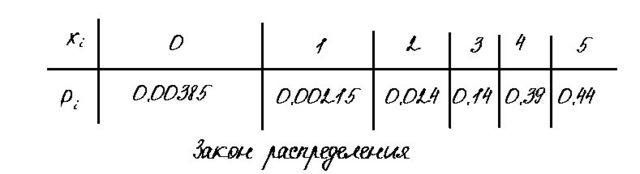Ответ:
Пошаговое объяснение:
1) Составим закон распределения случайной величины X

2) A — среди 5 животных будет не более 3 здоровых животных
 3)=1-C^4_5p^4(1-p)-p^5=0.16479" alt="P(A)=P(k\leqslant 3)=1-P(k>3)=1-C^4_5p^4(1-p)-p^5=0.16479" align="absmiddle" class="latex-formula">
3)=1-C^4_5p^4(1-p)-p^5=0.16479" alt="P(A)=P(k\leqslant 3)=1-P(k>3)=1-C^4_5p^4(1-p)-p^5=0.16479" align="absmiddle" class="latex-formula">
B — среди 5 животных не менее 5 здоровых животных

C — среди 5 животных не менее 3 и не более 4 здоровых

3) Наивероятнейшее число k определим из двойного неравенства

5 здоровых животных вероятнее всего будет среди 5 отобранных.
4)