Обчислити площу заштриховоної фігури y=x^3-3x+2. y=x+2

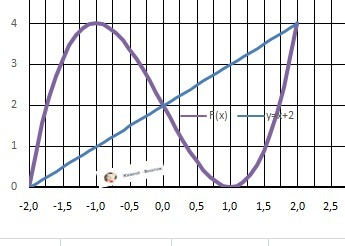
Ответ: S = 4.

ДАНО: y1 = x³ - 3*x + 2, y2 = x + 2

Найти: S=? - площадь.

Пошаговое объяснение:

1) Находим пределы интегрирования.

x+2 = x³ - 3*x +2

x³ - 4x = x*(x²-4) = x*(x-2)*(x+2) = 0.

Фигура справа - а = 2 - верхний предел, b = 0 - нижний предел.

2) Площадь - интеграл разности функций.

$\int\limits^2_0 {(4x-x^3)} \, dx=\frac{4x^2}{2}-\frac{x^4}{4}$

3) Вычисляем

S(2) = 2*2² - 2⁴/4 = 8 - 4 = 4, S(0) = 0

S = S(2) - S(0) = 4 - площадь.

Рисунок к задаче в приложении.