Построить график и иследовать функцию у=x/(x+2)^2 СРОЧНО.

Пошаговое объяснение:

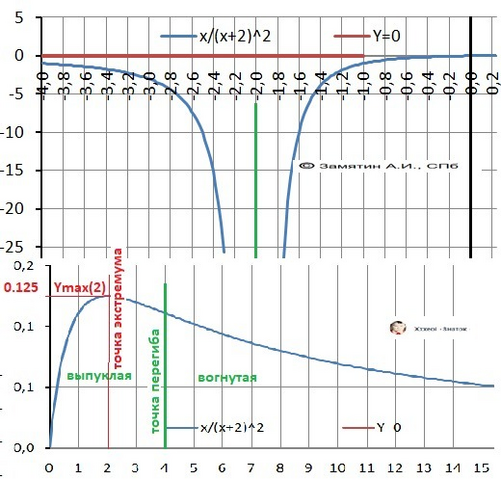
1. Разрыв при Х = -2.

2) Y(0) = 0 - пересечение с осью У

3) Пересечения с осью Х - нет.

4) Первая производная.

$Y'(x)=\frac{1}{(x+2)^2}-\frac{2x}{(x+2)^3}=0$

5) Локальный экстремум: Ymax(2) = 1/8 = 0.125

5) Вторая производная.

$Y"(x)=-\frac{4}{(x+2)^3}+\frac{6x}{(x+2)^4}=0$

6) Точка перегиба Х = 4.

7) Рисунок с графиком функции в приложении.