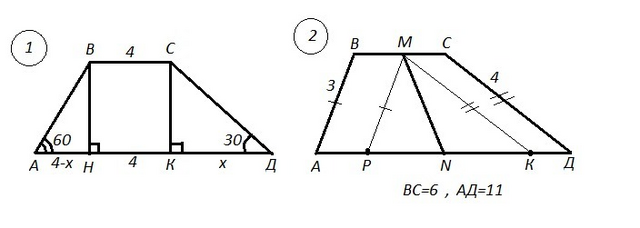
1) АВСД - трапеция , АД=8 см , ВС=4 см , ∠АДС=30° , ∠ВАД=60° .
Проведём ВН⊥АД и СК⊥АД . Получим прямоугольные треугольники АВН и СДК. ВСКН - прямоугольник , так как ВН║СК (если два перпендикуляра проведены к одной прямой, то они между собой будут параллельны) и ВС║НК, так как это основания трапеции) .
ВС=НК=4 см , ВН=СК. Обозначим КД=х , тогда АН=АД-НК-КД=8-4-х=4-х
ΔАВН: ∠АНВ=90° , ∠А=60° . (4-х)/АВ=cos60° ⇒ AB=(4-x)/cos60°=(4-x)/(0,5)=2(4-x).
BH/AB=sin60° ⇒ BH=ABsin60°=2(4-x)·√3/2=√3·(4-x) .
ΔСКД: ∠СКД=90° , ∠СДК=30° ,
х/CД=cos30° ⇒ CД=x/cos30°=x/(√3/2)=2x/√3 .
CK/СД=sin30° ⇒CK=СД·sin30°=(2x/√3)·(1/2)=x/√3 .
BH=CK ⇒ х/√3=√3·(4-x) ⇒ 3(4-x)=x , 12-3x=х , 4x=12 , х=3 .
КД=х=3 см , АВ=2(4-х)=2(4-3)=2 см , СД=2х/√3=2·3/√3=2√3 см.
2) АВСД - трапеция , ВС=6 см , АД=11 см , АВ=3 см , СД=4 см .
ВМ=МС , AN=NД . Найти MN.
Проведём два отрезка из точки М, параллельно боковым сторонам. Получим отрезки МР║АВ , МК║СД . А также получим два параллелограмма АВМР и ДСМК ⇒ МР=АВ=3 см , МК=СД=4 см .
Рассмотрим ΔРМК. РК=АД-(АР+КД)=АД-(ВМ+МС)=АД=ВС=11-6=5 (см).
Получили ΔРМК со сторонами 3 см , 4 см , 5 см . Это прямоугольный треугольник с катетами 3 см и 4 см и гипотенузой 5 см: 3²+4²=5² .
∠РМК=90° ⇒ МN - медиана прямоугольного треугольника, проведённая из прямого угла. По известной теореме она равна половине гипотенузы, то есть MN=1/2·РК=1/2·5=2,5 (см) .