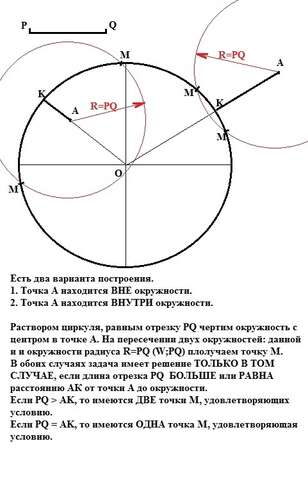
Есть два варианта построения.
1. Точка А находится ВНЕ окружности.
2. Точка А находится ВНУТРИ окружности.
Соединим данную нам точку А с центром данной нам окружности прямой АО, которая пересечет окружность а точке К. АК - это расстояние от точки К до окружности. Раствором циркуля, равным отрезку PQ чертим окружность с центром в точке А. На пересечении двух окружностей: данной и окружности радиуса R=PQ (W;PQ) плолучаем точку М.
В обоих случаях задача имеет решение ТОЛЬКО В ТОМ СЛУЧАЕ, если длина отрезка PQ БОЛЬШЕ или РАВНА расстоянию АК от точки А до окружности.
Если PQ > AK, то имеются ДВЕ точки М, удовлетворяющих данному условию (АМ=PQ).
Если PQ = AK, то имеются ОДНА точка М, удовлетворяющая данному условию (AM=PQ).