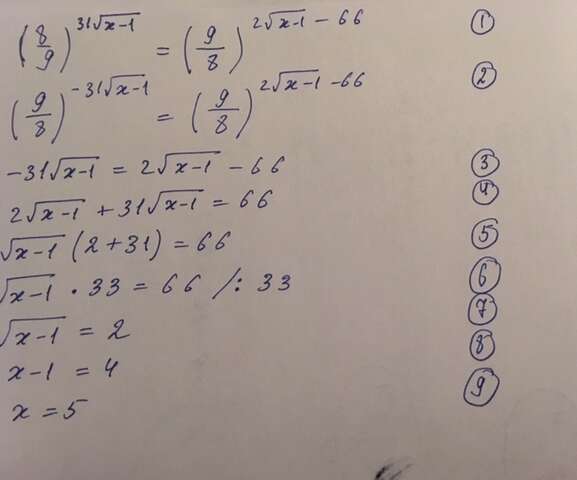Ответ: 5
^ - знак степени
§ - знак корня (только в данной задаче)
* - знак умножения
Сначала нужно привести основания степени в одинаковый вид. Для этого представим дробь 8/9 как (9/8)^(-1). Таким образом получается(2):
(9/8)^(-1) * 31§(x-1) = (9/8)^(2§(x-1)-66), а впоследствии получается
(9/8)^(-31§(x-1)) = (9/8)^(2§(x-1)-66)
Так как основания теперь одинаковы, то логично, что для равенства этих выражений должны быть равны их степени(3):
-31§(x-1) = 2§(x-1)-66
Переносим всё, что с корнем, в одну сторону, без корня - в другую(4):
2§(x-1) + 31§(x-1) = 66
Выносим корень за скобку (сокращать на него нельзя ни в коем случае)(5):
§(х-1) * (2 + 31) = 66
§(х-1) * 33 = 66
Сокращаем обе части на 33 (6):
§(х-1) = 2
Возводим обе части в квадрат, чтобы избавится от корня в левой части равенства (8):
х-1 = 4
х = 5