Основания призмы лежат в параллельных плоскостях, две параллельные плоскости пересекаются третьей - линии пересечения параллельны, BD||MN, BDMN - трапеция.
Боковые ребра призмы параллельны и равны, BB1D1D - параллелограмм, BD||B1D1 => MN||B1D1. M - середина B1C1 => MN - средняя линия △B1C1D1, N - середина C1D1. Грани данной призмы - равные ромбы. BB1=DD1, ∠BB1C1=∠DD1C1, B1M=D1N => △BB1C1=△DD1C1 (по двум сторонам и углу между ними), BM=DN
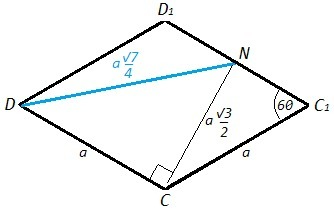
△BAD - равнобедренный с углом 60 => равносторонний, BD=a. B1D1=BD=a (BB1D1D - параллелограмм), MN=B1D1/2=a/2 (MN - средняя линия △B1C1D1). Ромб с углом 60 составлен из двух равносторонних треугольников. Высота равностороннего треугольника со стороной a равна a√3/2. По теореме Пифагора:
DN=√(a^2 +3a^2/4) = a√7/2
Или по теореме косинусов:
BM^2= BB1^2 + B1M^2 -2 BB1*B1M*cos120 = a^2 +a^2/4 +a^2/2 =7/4 a^2 <=> BM= a√7/2