В плоскости квадрат ABCD проведена прямая SB перпендикуляр сторон AB,BC . точка S-...

Question

В плоскости квадрат ABCD проведена прямая SB перпендикуляр сторон AB,BC . точка S- соединена с вершиной А. Определить вид треугольника SAD . Найти длину отрезка SD , если сторона квадрата 4 см , а длина перпендикуляра SB 5см Помогите пожалуйста , очень нужно!

Answer 1

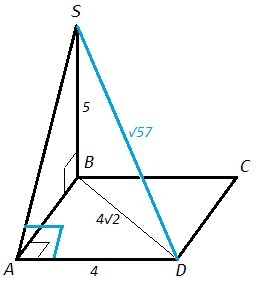
Прямая SB перпендикулярна двум пересекающимся прямым в плоскости ABC, следовательно перпендикулярна плоскости и любой прямой в этой плоскости. SB⊥BD. BD=4√2 (диагональ квадрата). По теореме Пифагора:

SD= √(SB^2 +BD^2) =√(25+32) =√57  

SB⊥BA, BA - проекция SA. Теорема о трех перпендикулярах: если прямая (AD), проведенная на плоскости через основание наклонной (SA), перпендикулярна ее проекции (AD⊥BA), то она перпендикулярна и самой наклонной (AD⊥SA). △SAD - прямоугольный.  

Проверка:

SA= √(SB^2 +AB^2) =√(25+16) =√41

57=41+16

---