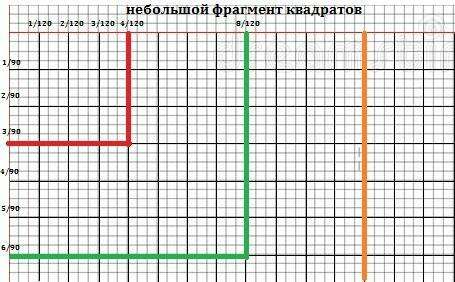
Пошаговое объяснение:
По условию есть квадрат со стороной 1, и его стороны ( которые равны) разбили на 120 равных частей по горизонтали и 90 равных частей по вертикали. Соответственно , по горизонтали получаем отрезки с минимальной величиной 1/120, а по вертикали 1/90.Отношение отрезков будет : 1/90 : 1/120 = 3:4. Значит 3 части по вертикали соответствуют по величине 4 частям по горизонтали. Можем записать : 3/90 = 4/120 – это будут стороны наименьшего квадрата.
Все последующие квадраты будут строиться по принципу +3/90 по вертикали и +4/120 по горизонтали. Мы получаем арифметическую прогрессию.
Формула арифметической прогрессии : an = a₁ + (n-1)*d
где аn- последний член арифметической прогрессии, a₁- первый член арифметической прогрессии,d- разность арифметической прогрессии, n- количество членов арифметической прогрессии.
Подставим наши данные
аn = 90/90; а₁ = 3/90; d = а₂ - а₁ = 6/90 - 3/90 = 3/90 ,
а теперь найдем n , что и будет количеством квадратов , на которые разбивается исходный квадрат
an = a₁ + (n-1)*d
90/90= 3/90+(n-1)*3/90
n-1= (90/90-3/90): 3/90
n= ((90/90-3/90):3/90)+1
n=1:1/30
n=30
На рисунке можно будет увидеть 30 разных квадратов
( рисунок во вложении )