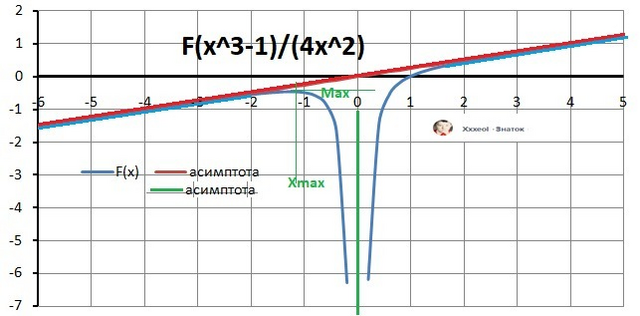
ДАНО: F= (x³+4)/x²
ИССЛЕДОВАНИЕ
1.Область определения D(x) - x²≠ 0 - разрыв при Х =0.
Х∈(-∞;0)∪(0;+∞).
2. Вертикальная асимптота - Х = 0.
3. Поведение в точке разрыва.
limF(o-) = - ∞, limF(o+) = - ∞
4. Нули функции - пересечение с осью Х.
x³-1 = 0 при х = 1.
5. Пересечение с осью У – нет – функция не существует.
6. Интервалы знакопостоянства.
Отрицательна: Х∈(-∞;0)∪(0;-1). Положительна: Х∈(1;+∞).
7. Наклонная асимптота. Уравнение: lim(∞)(k*x+b – f(x).
Y(x) = (x -1/x²)/4 = x. (Разделили на х² - степень знаменателя)
Y(x) = 1/4* x - уравнение наклонной асимптоты .
8. Исследование на чётность.
Y(-x) = (-x³-1)/(4*x²) ≠ - Y(x). Y(-x) = -(-x³+4)/x² ≠ - Y(-x).
Думаем: в формуле и чётные степени и нечётные - вывод:
Функция ни чётная ни нечётная.
9. Поиск экстремумов - в корнях первой производной
Запишем функцию в виде произведения: Y(x) = (x³+1) * (4*x²)⁻¹.
Y’(x) = 1/4 + 1/(2*x³) = 0
, упрощаем: 2*x³= -4, x=∛(-2), x≈ -1.26 - решение.
10. Локальные экстремумы.
Максимум – Хmax = y(∛-2) = -3/(4*∛2) ≈ - 0,47. Минимума – нет.
11. Интервалы монотонности.
Возрастает: X∈(-∞;Xmax)∪(0;+∞), убывает - Х∈(Xmax;0)
12. Вторая производная - Y"(x) = -3/(2*x⁴) = 0.
13. Точек перегиба - нет (Только в точке разрыва - Х =0)
Выпуклая – «горка» Х∈(-∞;-0)∪(0;+∞).
14. Область значений Е(у) У∈(-∞;+∞)
15. График в приложении