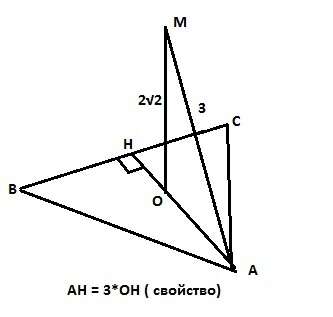
В правильном треугольнике высоты, медианы и биссектрисы равны, а центр треугольника делит их в отношении 2:1, считая от вершины. Рассмотрим треугольник АОМ. Перпендикуляр ОМ - катет, отрезок АМ (расстояние от точки М до вершины А) - гипотенуза. Тогда отрезок АО по Пифагору равен АО=√(АМ²-МО²) = √(9-8) =1. А так как АО = 2/3 высоты треугольника, то высота эта равна 1*3/2 = 1,5.
Ответ: высоты треугольника АВС равны 1,5 ед.
Как, в прочем, медианы и биссектрисы.