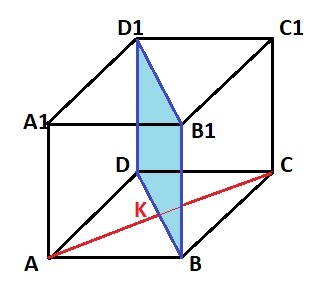
Задача 2.25. - рисунок к задаче в приложении.
Ребро ВВ1 ⊥ ВС ⇒плоскость BB1D1D ⊥ ABCD
Диагонали в основании АС ⊥BD - квадрат.
Теорема о трёх перпендикулярах - если прямая перпендикулярна двум пересекающимся на плоскости прямым, то он а перпендикулярна всей плоскости BB1D1C.
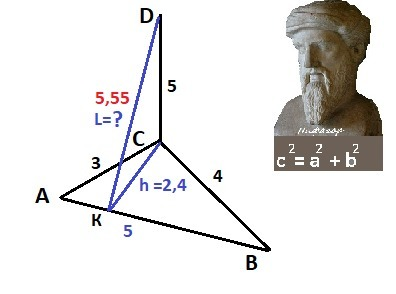
Задача 2.26. - рисунок к задаче в приложении.
По теореме Пифагора длина гипотенузы АВ. ("египетский треугольник"
c = √(4²+3²) = 5 - гипотенуза АВ.
Высота h(c) в треугольнике по трем сторонам по формуле:

h² = 2.4² = 5.76 - катет, CD = 5 - катет,
DK² = 25 + 5.76 = 30.76
DK = √30.76 ≈ 5.546 - расстояние до гипотенузы - ОТВЕТ
°