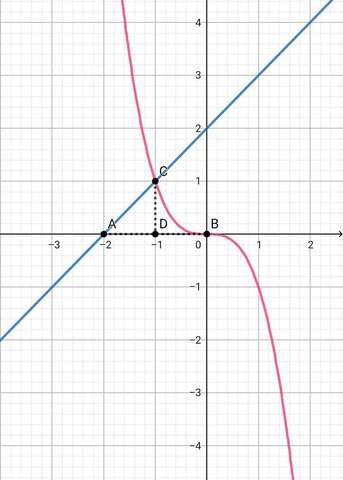
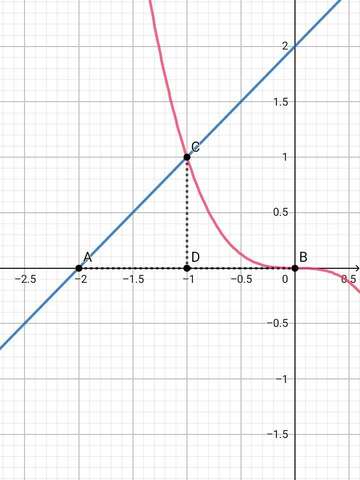
Найдите площадь фигуры, ограниченной линиями у = - х³, у = 0 и у = 2 + х.
РЕШЕНИЕ:

степенная функция, графиком которой является кубическая парабола, проходящая из || координатной четверти в |V четверть ( розовая кривая )

линейная функция, графиком которой прямая, проходящая из | коорд. четверти в ||| четверть ( синяя прямая )

это вся ось Ох
--------------------------------------------------
Нарисуем эти линии и найдём абсциссы точек их пересечения, приравняв правые части функций у = - х³ и у = х + 2.

Из первой скобки получаем х = - 1 , а вторая скобка действительных корней не имеет.
Искомая площадь фигуры АВС может быть получена как сумма площадей криволинейной трапеции ВСD и треугольника ACD.
Найдём первообразную функции у = - х³:
F(x) = - x^4 / 4 + C
По формуле Ньютона - Лейбница:
S = F(b) - F(a)
S bcd = F( 0 ) - F( - 1 ) = - 0^4 / 4 - ( - ( - 1 )^4 / 4 ) = 1 / 4 = 0,25
S acd = AD • CD / 2 = 1 • 1 / 2 = 1 / 2 = 0,5
Следовательно, площадь фигуры АВС равна:
S abc = S bcd + S acd = 0,25 + 0,5 = 0,75
ОТВЕТ: 0,75