Ответ:
Пошаговое объяснение:
а) По теореме Пифагора вычисляем длины сторон треугольника.
L² = ΔY³ + ΔX²
L(AB) = √(4 + 64) = √68 = 8.25
L(BC) = √(4 + 64) = √68 = 8.25 - стороны равны.
L(AC) = √(16 +0) = 4
б) Точка М - медианы по середине отрезка АС.
М = (А+С)/2 - формула вычисления середины отрезка.
Мх = 3, Му = - 2. М(3;-2)
Длина медианы ВМ = √(0+64) = 8 - это и высота треугольника.
Площадь по формуле:
S = AC*BM /2 = 4 * 8 /2 = 16 - площадь - ответ.
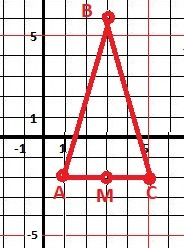
Рисунок к задаче в приложении.