Ответ:
10,7
Пошаговое объяснение:
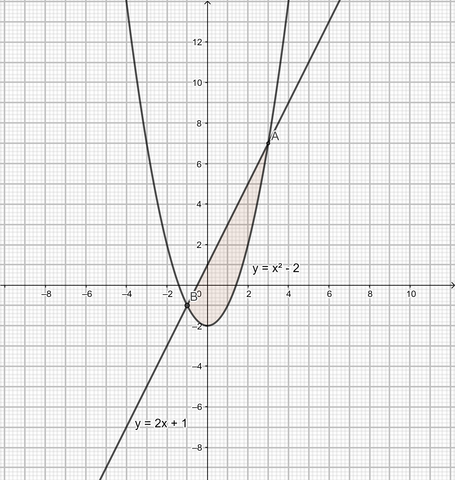
Требуется вычислить площадь, заключенную между параболой y=x^2-2 и прямой y=2x+1.
Найдем точки пересечения параболы и прямой:
![\[\left\{ \begin{array}{l}y = {x^2} - 2\\y = 2x + 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2x + 1 = {x^2} - 2\\y = 2x + 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2x + 1 - {x^2} + 2 = 0\\y = 2x + 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - {x^2} + 2x + 3 = 0\\y = 2x + 1\end{array} \right.\]% MathType!End!2!1! \[\left\{ \begin{array}{l}y = {x^2} - 2\\y = 2x + 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2x + 1 = {x^2} - 2\\y = 2x + 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2x + 1 - {x^2} + 2 = 0\\y = 2x + 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - {x^2} + 2x + 3 = 0\\y = 2x + 1\end{array} \right.\]% MathType!End!2!1!](https://tex.z-dn.net/?f=%5C%5B%5Cleft%5C%7B%20%5Cbegin%7Barray%7D%7Bl%7Dy%20%3D%20%7Bx%5E2%7D%20-%202%5C%5Cy%20%3D%202x%20%2B%201%5Cend%7Barray%7D%20%5Cright.%20%5CLeftrightarrow%20%5Cleft%5C%7B%20%5Cbegin%7Barray%7D%7Bl%7D2x%20%2B%201%20%3D%20%7Bx%5E2%7D%20-%202%5C%5Cy%20%3D%202x%20%2B%201%5Cend%7Barray%7D%20%5Cright.%20%5CLeftrightarrow%20%5Cleft%5C%7B%20%5Cbegin%7Barray%7D%7Bl%7D2x%20%2B%201%20-%20%7Bx%5E2%7D%20%2B%202%20%3D%200%5C%5Cy%20%3D%202x%20%2B%201%5Cend%7Barray%7D%20%5Cright.%20%5CLeftrightarrow%20%5Cleft%5C%7B%20%5Cbegin%7Barray%7D%7Bl%7D%20-%20%7Bx%5E2%7D%20%2B%202x%20%2B%203%20%3D%200%5C%5Cy%20%3D%202x%20%2B%201%5Cend%7Barray%7D%20%5Cright.%5C%5D%25%20MathType%21End%212%211%21)

Найдем дискриминант квадратного уравнения:




Подставим x в уравнение:
y₁=7; y₂=-1
Получаем две точки пересечения : (3;7) и (-1;-1)
Пределы интегрирования a=-1, b=3. Площадь фигуры равняется:





Графики прилагаются.