В общем-то, в чём заключается логика: площадь территории, объеденной козлом, будет иметь форму круга, ибо он привязан на верёвку. Поскольку колышек стоит ровно по центру, а диаметр круга больше стороны огорода, то часть круга будет выходить за пределы огорода (т.е. козёл будет упираться в стенки огорода). Следовательно, алгоритм действий следующий: находим площадь круга, используя длину верёвки в качестве радиуса, затем находим площадь секторов, выходящих за пределы огорода и вычитаем их.
В конечном счёте формула должна выглядеть так:
- длина верёвки
- угол сегмента, сектор которого выходит за пределы огорода
Очевидно, что необходимо каким-то образом вычислить этот угол
Вы попросили только формулу, поэтому дальнейшее решение я не буду расписывать подробно, но угол этот равен приблизительно 66°68'
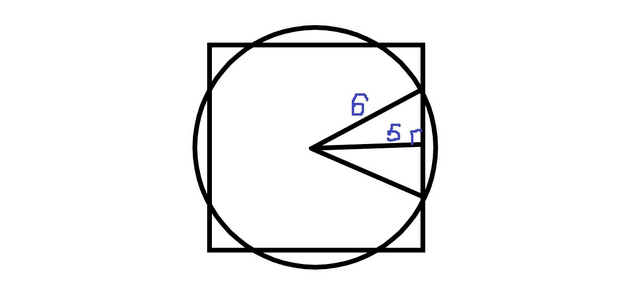
Угол можно найти, решив эту задачу (картинка)
