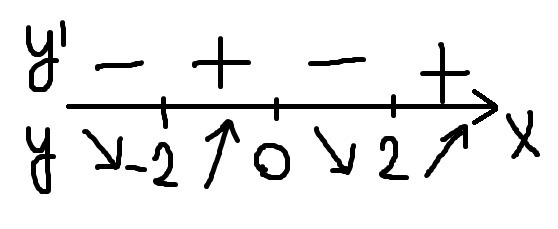y = x⁴ - 8x² + 3 [-2;2]
1. D(y) = {x | x ∈ R}
2. y'(x) = 4x³ - 16x = 4x(x² - 4) = 4x(x+2)(x-2)
3. y'(x) = 0
4x(x+2)(x-2) = 0 => x = 0 или x = -2 или x = 2
Все значения x принадлежат отрезку [-2;2]
4. Приложение 1
y(x) убывает на (-∞;2)∪(0;2)
y(x) возрастает на (-2;0)∪(2;+∞)
5. f(-2) = 16 - 8*4 + 3 = -13 ; f(0) = 3 ; f(2) = -13
Точка максимума функции y(x) на отрезке [-2;2] равна 3.
Точка минимума функции y(x) на отрезке [-2;2] равна -13.