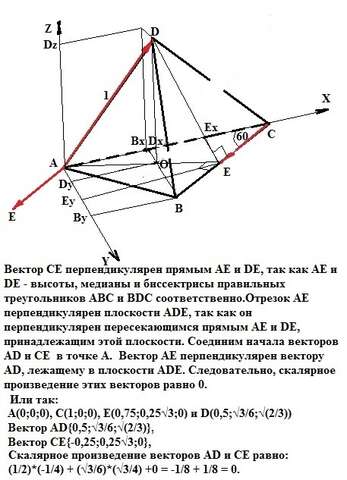
Вектор СЕ перпендикулярен прямым АЕ и DE, так как АЕ и DE - высоты, медианы и биссектрисы правильных треугольников АВС и BDC соответственно.Отрезок АЕ перпендикулярен плоскости ADE, так как он перпендикулярен пересекающимся прямым АЕ и DE, принадлежащим этой плоскости. Соединим начала векторов AD и СЕ в точке А. Вектор АЕ перпендикулярен вектору AD, лежащему в плоскости ADE. Следовательно, скалярное произведение этих векторов равно 0.
Или так:
Скалярное произведение векторов a и b равно сумме произведений соответствующих координат этих векторов.
a·b = (Xa*Xb+Ya*Yb+Za*Zb)
Применим координатный метод.
Привяжем систему декартовых координат к вершине А нашего правильного тетраэдра. Тетраэдр правильный, следовательно, его основание (и все боковые грани) - правильный треугольник. Высота правильного треугольника по формуле равна ВBx=(√3/2)*а, где а - сторона треугольника. В нашем случае а=1. Тогда точка В(0,5;√3/2;0). Отрезок ЕEx из треугольника ЕЕхС равен ЕЕх=СЕ*Sin60 = 0,25√3. CEx=CE*Cos60 = 0,25. Отрезок АЕх=1-0,25 = 0,75. Значит точка Е(0,75;0,25√3;0)
Вершина тетраэдра D проецируется в центр основания, который делит высоту (медиану) основания в отношении 2:1, считая от вершины. Значит координата Dy = (1/3)*By = √3/6.
Высота правильного тетраэдра равна по Пифагору DO=√(DB²-BO²) или, зная что ВО = (2/3)*By, DO=√(1-1/3)=√(2/3) = Dz.
Тогда точка D(0,5;√3/6;√(2/3)).
Итак, имеем точки с координатами:
А(0;0;0), С(1;0;0), Е(0,75; 0,25√3; 0) и D(0,5; √3/6; √(2/3)).
Вектор AD{0,5;√3/6;√(2/3)}, Модуль его нам дан, он равен 1. Но для проверки полученных координат вектора, найдем модуль по формуле: |AD| = √(ADx²+ADy²+ADz²) = √(1/4+1/12+2/3)=√1 =1.
Вектор CE{-0,25;0,25√3;0}, Модуль его нам дан, он равен 0,5. Но для проверки полученных координат вектора, найдем модуль по формуле: |CE| = √(CEx²+CEy²+CEz²) = √(0,0625+0,0625*3+0)=√0,25=0,5.
Тогда AD*CE=(0,5*(-0,25)+(√3/6)*(0,25√3)+0) = 0.
Ответ: скалярное произведение векторов AD и СЕ равно 0.