Пошаговое объяснение:
Рисунок к задаче в приложении.
Площадь треугольника по формуле: S =a*h/2, где: а - основание, h - высота. Задача сводится - провести прямую на расстоянии h. Таких прямых будет две.
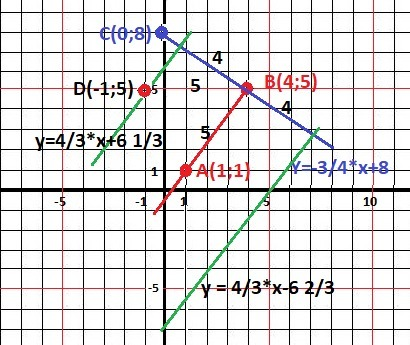
Находим длину основания - АВ по теореме Пифагора.
а² = (By -Ay)² + (Bx - Ax)² = 4²+3² = 25, a = 5 - основание.
h = 2*S/a = 20: 5 = 4 - высота
Уравнение прямой АВ.
1) k = ΔY/ΔX = (Ay-By)/(Ax-Bx)=(1-(5))/(1-(4))= 4/3 = 1,33 - наклон прямой
2) b=Ay-k*Ax=1-(1,33)*1= - 1/3 = -0,33- сдвиг по оси ОУ
Уравнение Y(AB) = 4/3*х - 1/3 ≈ 1,33*x - 0,33
Переносим точку B на 5 единиц (станет гипотенузой) , чтобы получить катет = 4
Точка D(-1,5), наклон k = 4/3 = 1,33
b = Dу - k*Dx = 5 - (1,33)*(-1) = 6,33
Уравнение прямой - Y(D) = 4/3*x + 6 1/3 = 1,33*x + 6,33 - ответ
Уравнение прямой - Y(Е) = 4/3x - 6 2/3 - ответ