Помогите пожалуйста!!! Исследовать функцию y= x^2+3/2x+1 по следующей схеме: 1) Найдите...

Question

Помогите пожалуйста!!! Исследовать функцию y= x^2+3/2x+1 по следующей схеме: 1) Найдите область определения функции 2)Исследовать функцию на непрерывность 3) Определить, является ли данная функция четной, нечетной( сделать вывод о наличии или отсутствии симметрии) 4) найти интервалы монотонности и точки экстремума 5) найти интервалы выпуклости и вогнутости графика функции и точки перегиба 6) найти точки пересечения графика с осями координат По результатам построить график

Comments

Уточните: y = (x^2+3)/(2x+1) или у = x^2 + 1.5*x + 1

Answer 1

ДАНО:  

Исследование:

1. Область определения D(y).  В знаменателе: 2*х+1 ≠0,  х≠ - 0,5

Х∈(-∞;-0,5)∪(-0,5+∞) -

2, Непрерывность функции:  разрыв при Х=-0,5.

Вертикальная асимптота: х = -0,5.

3. Проверка на чётность.

Y(-x) = (x²+3)/(-2*x+1) ≠ - Y(x) ≠ Y(x)

Функция ни чётная ни нечётная.

Вывод:  нет ни осевой симметрии, как у функции y = x²,  ни центральной, как у функции y= x³

4. Пересечение с осью OХ.   Y(x) = 0 - нет.

5. Интервалы знакопостоянства.

Отрицательная - Y(x)<0 X=(-oo;-0,5]  </p>

Положительная -Y(x)>0 X=[-0,5;+oo)

6. Пересечение с осью OY. Y(0) = 3.

7. Поиск экстремумов по первой производной.

Корни Y'(x)= 0.     Х4= 2x/2x = 1   Х5=  ? (≈-2.25)

7. Локальные экстремумы.  

Минимум  Ymin(X4= 1) =4/3.   Максимум Ymin(X5=8,36) = ?

8. Интервалы возрастания и убывания.  

Возрастает Х=(-оо; x5]U[1;+oo) , убывает - Х=[x5;-0.5)∪(0.5;1]

9. Вторая производная

Корней производной - нет. Точка перегиба в точке разрыва при Х=-0,5

10. Выпуклая “горка» Х∈(-∞; -0,5)

Вогнутая – «ложка» Х∈(-0,5; +∞).

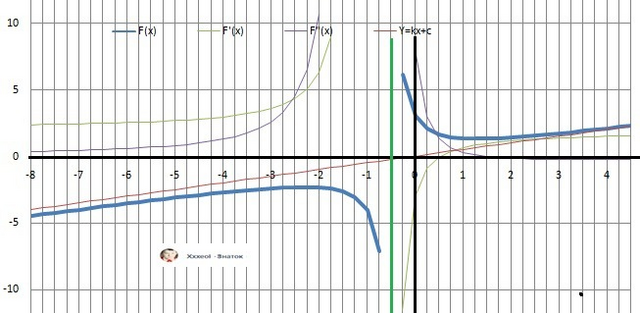
11. График в приложении.

---