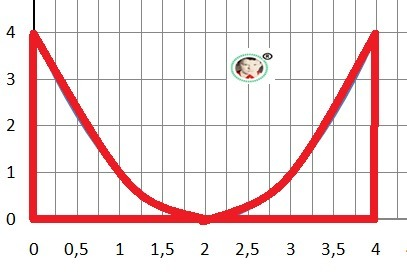
Ответ: Площадь 5 1/3.
ДАНО:
y1(x) = x²-4*x+4, y2(x) = 0
a = x = 4 - верхний предел
b = y =0 - нижний предел.
Найти: S=? - площадь.
Решение.
Площадь - интеграл разности функций:
s(x) = (4 - 4*x - x²) - 0 - подынтегральная функция.
Интегрируем.

(Мне нравится именно такая запись интеграла - понятен принцип получения формулы. Степень при Х увеличивается на 1, а число делится на значение этой степени.)
Вычисляем на границах интегрирования.
S(0) = 0.
S(4) = 16 - 32 + 21 1/3 = 5 1/3 - площадь - ответ.