Площадь фигуры, ограниченной линиями
у=4 = х², у = 2 - х, и х = - 1, х = 1
представляет собой разность двух площадей
S₁ - площадь криволинейной трапеции ограниченной сверху линией параболы у=4 = х², слева и справа прямыми х = - 1, х = 1 и снизу осью ОХ у=0.
S₂ площадь прямоугольной трапеции ограниченная сверху графиком прямой у - 2 - х, слева и справа прямыми х = - 1, х = 1 и снизу осью ОХ у=0.
S = S₁ - S₂
Нужная площадь равна разности этих площадей.
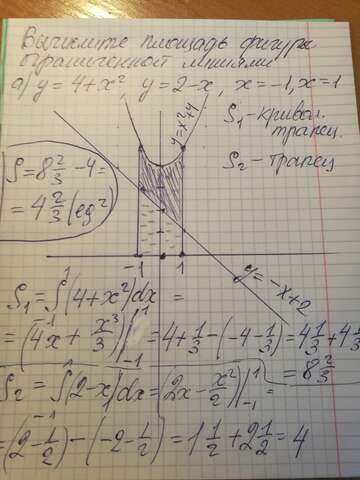
Известно, что такая площадь находится как определенный интеграл. Решение на фото