В кубе ABCDA1B1C1D1 сторона основания равна 3 см. найдите площадь сечения A1B1CD. В...

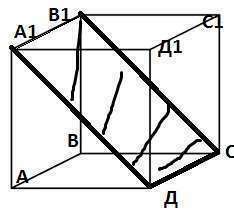
У куба все стороны равны.
Нужно найти площадь сечения
А1Д = В1С
Эти стороны сечения можно найти по теореме Пифагора:
$A1D = \sqrt{ (AA1)^{2} + (AD)^{2} } = \sqrt{9+9} = \sqrt{18} = 3 \sqrt{2}$

Sсеч = А1Д * ДС = 3√2 * 3 = 9√2 см²

В ответе укажите число равное произведению найденной площади на корень из 2
(Здесь не совсем поняла, так нужно сделать?)

9√2 * √2 = 9*2 = 18