Задание 3.1
Очень внимательно прочитали.
Задание 3.2
Я так понял, умножение - это конъюнкция. Преобразуем формулу в понятную более менее для глаз:
F = x₁ && x₂ || x₃ || x₁ && (x₂ || x₃) && ¬x₁
Обозначим некоторые функции переменными:
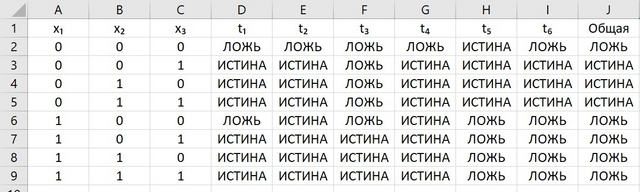
t₁ = x₂ || x₃=ИЛИ(B2; C2)
t₂ = x₁ || t₁ =ИЛИ(A2; ИЛИ(B2; C2))
t₃ = x₁ && t₁=И(A2; ИЛИ(B2; C2))
t₄ = t₂ || t₃ =ИЛИ(ИЛИ(A2; ИЛИ(B2; C2)); И(A2; ИЛИ(B2; C2)))
t₅ = ¬x₁ =НЕ(A2)
t₆ = t₄ && t₅ =И(ИЛИ(ИЛИ(A2; ИЛИ(B2; C2)); И(A2; ИЛИ(B2; C2))); НЕ(A2))
«Общая» =И(ИЛИ(ИЛИ(A2; ИЛИ(B2; C2)); И(A2; ИЛИ(B2; C2))); НЕ(A2))
t₆ - это конечная формула, а столбик «Общая» уже имеет в себе общую формулу, эта формула не описывает этапы (добавил её чисто для проверки своих выводов формул).
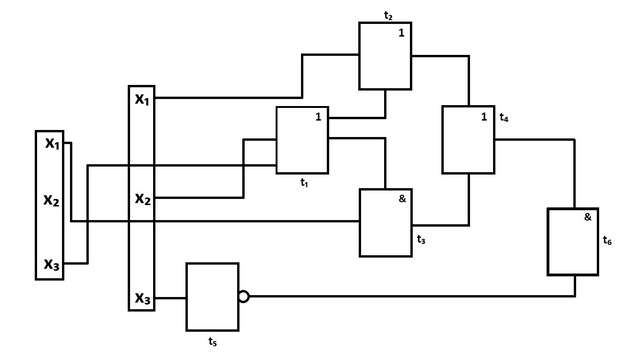
Логическую схему построил. Извини, если очень запутанно.
Задание 3.3
Я так понял, что нужно СКНФ и СДНФ. Тогда начнём с СКНФ. Всё очень просто. Для каждых x мы записываем конъюнкцию, если функция равна нулю. Если какой-нибудь из x равен единице - берётся с инверсией.
F(x₁, x₂, x₃) = (x₁ ∨ x₂ ∨ x₃) ∧ (x₁ ∨ ¬x₂ ∨ x₃) ∧ (¬x₁ ∨ ¬x₂ ∨ ¬x₃)
СКНФ делается абсолютно наоборот. Для каждой пары x записывем дизъюнкцию, но при условии, что эта пара x даёт функцию, равная единице. Если какой-нибудь x равен нулю - инверсия.
F(x₁, x₂, x₃) = (¬x₁ ∧ ¬x₂ ∧ x₃) ∨ (¬x₁ ∧ x₂ ∧ x₃) ∨ (x₁ ∧ ¬x₂ ∧ ¬x₃) ∨ (x₁ ∧ ¬x₂ ∧ x₃) ∨ (x₁ ∧ x₂ ∧ ¬x₃)