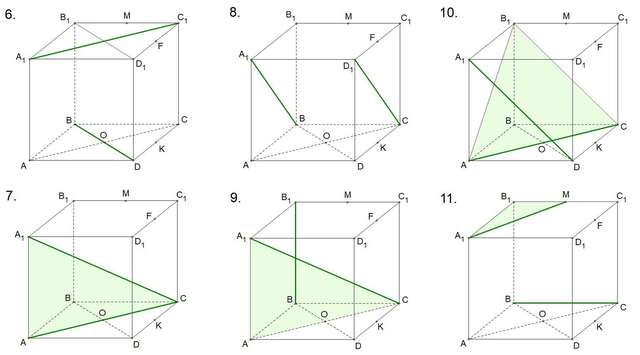
6. Скрещивающиеся. 90°
Прямые лежат на параллельных плоскостях (основания куба) и при этом не параллельны ⇒ A₁C₁ и BD скрещиваются.
"Перенесём" прямую BD в верхнее основание, то есть проведём (или найдём) в нём прямую, параллельную BD. В нашем случае это прямая B₁D₁.
Тогда ∠(A₁C₁, BD) = ∠(A₁C₁, B₁D₁) = 90° (диагонали квадрата перпендикулярны)
7. Пересекаются. arctg (1/√2)
Прямые A₁C и CA имеют общую точку C ⇒ они пересекаются. ∠(A₁C, CA) = ∠A₁CA
Пусть AB = a.
Рассмотрим ΔA₁CA. Он прямоугольный (AA₁⊥(ABC) ⇒ AA₁⊥AC).
AC -- диагональ квадрата, AC = a√2.
tg∠A₁CA = AA₁/AC = a/a√2 = 1/√2 ⇒ ∠A₁CA = arctg (1/√2)
8. Параллельные. 0°
Прямые лежат на параллельных плоскостях (могут быть параллельными или скрещивающимися). В данном случае видно, что они параллельны (для строго доказательства можно одну прямую перенести к другой и рассмотреть их на одной плоскости).
Угол между параллельными прямыми равен 0°.
9. Скрещивающиеся. arctg √2
BB₁ ⊂ (ABB₁), A₁C ∩ (ABB₁) = A₁ (прямая A₁C пересекает плоскость в точке A₁), A₁ ∉ BB₁ ⇒ прямые BB₁ и A₁C скрещивающиеся (по признаку скрещ. прямых).
∠(BB₁, A₁C) = ∠(AA₁, A₁C) = ∠AA₁C
Рассмотрим ΔAA₁C:
Он прямоугольный, AA₁ = a, AC = a√2 (пункт 7), тогда
tg∠AA₁C = AC/AA₁ = a√2/a = √2 ⇒ ∠AA₁C = arctg √2
10. Скрещивающиеся. 60°
AC ⊂ (ABC), A₁D ∩ (ABC) = D, D ∉ AC ⇒ прямые AC и A₁D скрещивающиеся (по признаку скрещ. прямых).
∠(AC, A₁D) = ∠(AC, B₁C) = ∠B₁CA
Рассмотрим ΔB₁CA: его стороны -- это диагонали равных квадратов, то есть все стороны равны и треугольник равносторонний.
Все углы в равностороннем треугольнике равны 60°.
11. Скрещивающиеся. arctg 2
Прямые лежат на параллельных плоскостях (могут быть параллельными или скрещивающимися). Если перенести одну из прямых к другой, то они пересекутся. Значит прямые A₁M и BC скрещивающиеся.
∠(A₁M, BC) = ∠(A₁M, B₁C₁) = ∠B₁MA₁
Рассмотрим ΔB₁MA₁:
Он прямоугольный (квадрат),
B₁A₁ = a, M -- середина B₁C₁ ⇒ B₁M = a/2, откуда
tg∠B₁MA₁ = B₁A₁/B₁M = a/(a/2) = 2a/a = 2 ⇒ ∠B₁MA₁ = arctg 2
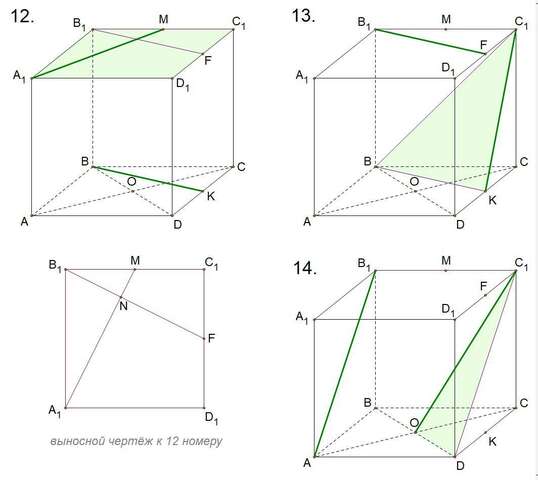
12. Скрещивающиеся. 90°
Прямые лежат на параллельных плоскостях (могут быть параллельными или скрещивающимися). Если перенести одну из прямых к другой, то они пересекутся. Значит прямые A₁M и BK скрещивающиеся.
∠(A₁M, BK) = ∠(A₁M, B₁F) = ∠B₁NA₁
Рассмотрим ΔA₁B₁M и ΔC₁B₁F:
1) A₁B₁ = C₁B₁ (квадрат)
2) ∠B₁ = ∠C₁ = 90° (квадрат)
3) B₁M = C₁F (M и F середины равных сторон)
Следовательно, ΔA₁B₁M = ΔC₁B₁F (по двум катетам) ⇒
⇒ ∠C₁B₁F = ∠B₁A₁M
∠A₁B₁F = ∠A₁B₁C₁ - ∠C₁B₁F = 90° - ∠C₁B₁F
Рассмотрим ΔA₁B₁N:
По теореме о сумме углов треугольника
∠A₁B₁N + ∠B₁A₁N + ∠B₁NA₁ = 180°
(90° - ∠C₁B₁F) + ∠C₁B₁F + ∠B₁NA₁ = 180°
∠B₁NA₁ = 90°
13. Скрещивающиеся. arccos √(1/5)
С₁K ⊂ (ABC), B₁F ∩ (DCC₁) = F, F ∉ С₁K ⇒ прямые С₁K и B₁F скрещивающиеся (по признаку скрещ. прямых).
∠(С₁K, B₁F) = ∠(С₁K, BK) = ∠С₁KB
BC₁ диагональ квадрата, BC₁ = a√2
BK = KC₁ (из равенства ΔBKC и ΔKCC₁)
Из ΔBKC по теореме Пифагора BK = a√5/2
Применим теорему косинусов к ΔBKC₁:
BC₁² = BK² + KC₁² - 2 * BK * KC₁ * cos∠K
(a√2)² = 2(a√5/2)² - 2(a√5/2)² * cos∠K
2a² = 5a²/2 (1 - cos∠K) | *2/5a²
1 - cos∠K = 4/5
cos∠K = 1/5 ⇒ ∠С₁KB = arccos (1/5)
14. Скрещивающиеся. 30°
С₁O ⊂ (ACC₁), B₁A ∩ (ACC₁) = A, A ∉ С₁O ⇒ прямые С₁O и B₁A скрещивающиеся (по признаку скрещ. прямых).
∠(С₁O, B₁A) = ∠(С₁O, C₁D) = ∠OС₁D
C₁O - наклонная, OC - проекция (CC₁⊥(ABC)), OC⊥BD ⇒ C₁O⊥BD
Рассмотрим ΔOC₁D:
Он прямоугольный (C₁O⊥BD), C₁D = a√2 (пункт 7), OD -- половина диагонали квадрата, OD = a√2/2, тогда
катет OD в 2 раза меньше гипотенузы C₁D ⇒ ∠OС₁D = 30° (по теореме об угле в 30 градусов в прямоугольном Δ)