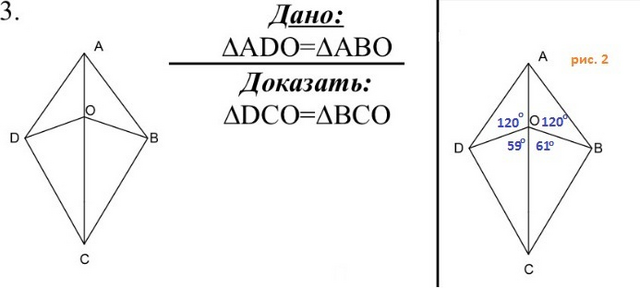
Задача имеет решение при условии, что точки A, O и C лежат на одной прямой, то есть ∠AOC = 180°. В противном случае треугольники вряд ли будут равны: ΔDCO≠ΔBCO. На рисунке 2 приведен пример углов, которые не являются смежными, но которые невозможно определить визуально.
=================================================
Итак, условие задачи.
Дано: O∈AC, ΔADO = ΔABO
Доказательство:
ΔADO = ΔABO ⇒ ∠AOD = ∠AOB - как тупые углы равных треугольников, OD = OB - как стороны, образующие тупые углы с общей стороной AO.
∠AOD + ∠СOD = 180° - смежные углы.
∠AOB + ∠COB = 180° - смежные углы.
∠AOD = ∠AOB ⇒ ∠COD = ∠COB
Рассмотрим ΔDCO и ΔBCO
OC - общая сторона, OD = OB, ∠COD = ∠COB
ΔDCO = ΔBCO по двум равным сторонам и углу между ними.