98 баллов на листочке по красоте сделайте. Буду признателен

Вычислить площадь треугольника, одна вершина которого совпадает с вершиной параболы y=x²-4, а две другие совпадают с точками пересечения этой параболы с осью абсцисс.

Способ №1 (без построения)

Найдем координаты вершины параболы:

$\sf x_0=\dfrac{-b}{2a}=\dfrac{0}{2}=0 \\ y_0=y(x_0)=0^2-4=-4$

Найдем нули функции (они и есть точки пересечения параболы с осью абсцисс)

$\sf x^2-4=0 \\ (x-2)(x+2)=0 \\ x=-2; \ x=2$

Обозначим треугольник ABC. Тогда его вершины: A(0; -4), B(-2; 0) C(2; 0).

Найдем длины сторон треугольника

$\sf AB=\sqrt{(-2-0)^2+(0-(-4))^2}=\sqrt{4+16}=\sqrt{20}=2\sqrt{5} \\ BC=\sqrt{(2-(-2))^2+(0-0)^2}=\sqrt{16}=4 \\ AC=\sqrt{(2-0)^2+(0-(-4))^2}=\sqrt{4+16}=\sqrt{20}=2\sqrt{5}$

Теперь находим полупериметр

$\sf p=\dfrac{2\sqrt{5}+2\sqrt{5}+4}{2}=2+2\sqrt{5}$

И по формуле Герона

$\sf S=\sqrt{(2+2\sqrt{5})(2+2\sqrt{5}-2\sqrt{5})^2(2+2\sqrt{5}-4)}=\sqrt{(2\sqrt{5}+2)\cdot 4(2\sqrt{5}-2)}= \\ = \sqrt{16\cdot4}=4 \cdot 2 =8$

Ответ: 8

Способ №2

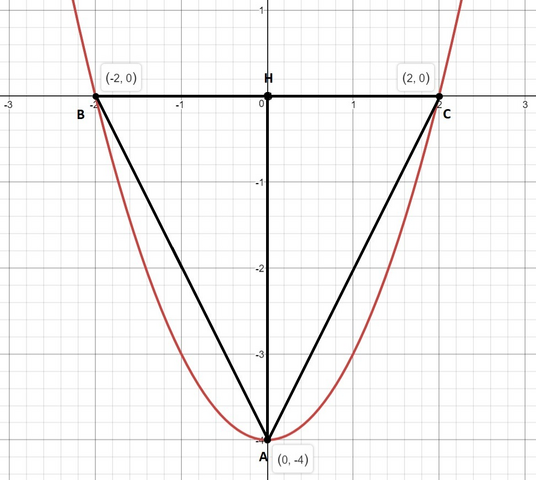
Строим график функции y=x²-4 по точкам и обозначаем нужный треугольник ABC. (в приложении)

Точки для графика: (-3; 5), (-2; 0), (0; -4), (2; 0), (3; 5)

Проводим в треугольнике высоту AH. Заметим, что основание треугольника равно 4, и высота равна 4. Тогда по формуле площади треугольника

$\sf S=\dfrac{1}{2}\cdot 4 \cdot 4=8$

Ответ: 8

98 баллов ** листочке по красоте сделайте. Буду признателен