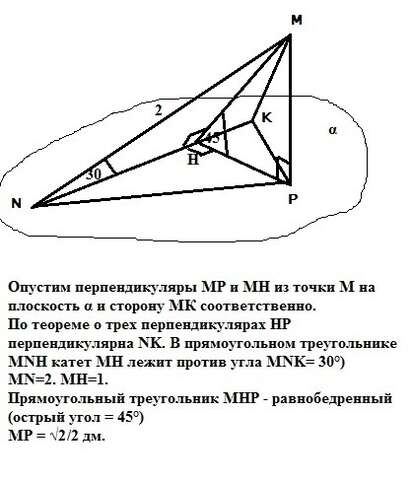
Опустим перпендикуляры МР и МН из точки М на плоскость α и сторону МК соответственно. По теореме о трех перпендикулярах НР перпендикулярна NK. Угол между двумя пересекающимися плоскостями равен углу между прямыми, по которым они пересекаются с любой плоскостью, перпендикулярной их линии пересечения. Значит угол между плоскостью α и плоскостью треугольника MNK - это угол МНР.
В прямоугольном треугольнике MNH катет МН лежит против угла MNK= 30°). => MN=2дм. MH=1дм.
Прямоугольный треугольник МНР - равнобедренный (острый угол = 45°). МР=НР, МН=1 дм. => МР = √2/2 дм.
Ответ: 1) 1дм, 2) √2/2 дм.