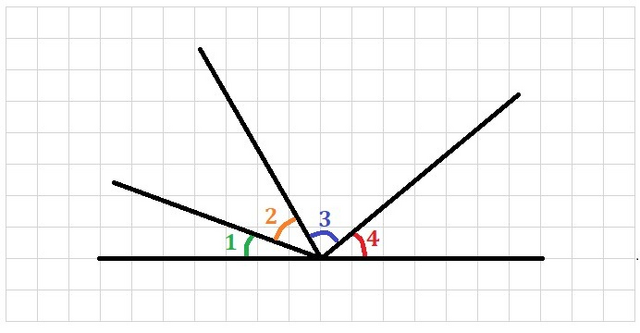
Задача на углы.
Решить задачу с помощью уравнения.
Развёрнутый угол разделим на 4 угла так, что один из них в 2 раза меньше второго и в 4 раза меньше третьего, но на 20° меньше четвёртого.
Найдите эти углы и выполните построение.
Рассмотрим условие.
- Развёрнутый угол имеет градусную меру 180°.
- Пусть угол, с которым идёт сравнение, то есть ∠1 = x градусов.
- Тогда угол ∠2 = 2x, третий угол ∠3 = 4x, и четвёртый ∠4 = (x + 20°) градусов.
Составим уравнение.
Сумма углов даст нам 180°, отсюда получаем уравнение.

Зная х без проблем находим все 4 угла.
∠1 = x = 20°;
∠2 = 2x = 2 × 30° = 40°;
∠3 = 4x = 4 × 30° = 80°;
∠4 = x + 20° = 30° + 20° = 40°.
Ответ: 20°, 40°, 80°, 40°.
* Построенные углы смотри в приложении.