Когда основы логарифма одинаковы, мы можем сравнить подлогарифмическое выражения :
ОДз:
х+7>1
х>-6
2 \\ log_{x + 7}(25) > log_{ \times + 7}( {(x + 7)}^{2} ) \\ 25 > {(x + 7)}^{2} " alt=" log_{x + 7}(25) > 2 \\ log_{x + 7}(25) > log_{ \times + 7}( {(x + 7)}^{2} ) \\ 25 > {(x + 7)}^{2} " align="absmiddle" class="latex-formula">
25 > х² +14х +49
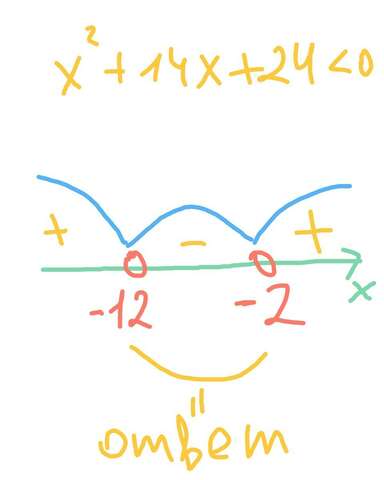
х²+14х+24<0<br>х²+14х+24=0
x²+12x +2x +24=0
x(x+12) +2(x+12)=0
(x+12)(x+2)=0
Корни : -12 и -2
Методом интервалов получаем:
Хє(-12;-2)
Учитывая ОДЗ
Ответ: Хэ(-6;-2)
