Ответ:
48
Пошаговое объяснение:
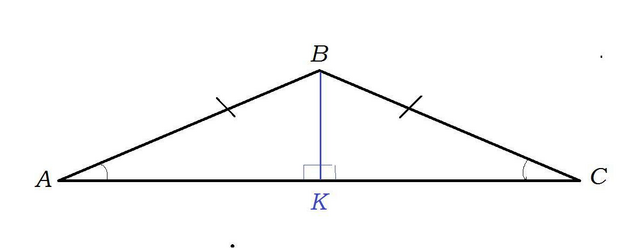
Дано: АВС --- треугольник.
АВ = ВС = 25
sin∠ВАС = 0,28
Найти: АС
Решение.
1. 1-ы й с п о с о б
Проведем из угла АВС высоту ВК
ΔАВК - прямоугольный ( по построению)
sin∠ВАС = ВК/АВ ---- по определению
ВК/АВ = ВК/25 = 0,28
ВК = 25 * 0,28 = 7
По теореме Пифагора АК = √(АВ² - ВК²) = √(25² - 7²) =√(625 - 49) = √576 = 24
Рассмотрим ΔВСК и ΔАВК. АВ = ВС -- по условию, ⇒ ∠ВАС = ∠ВСА - как углы при основании равнобедренного треугольника. ∠АВК = ∠СВК, - по свойству высоты равнобедренного треугольника ⇒ΔВСК =ΔАВ -- по второму признаку ⇒ АК = СК = 24
АС = АК + СК = 24*2 = 48
Ответ: 48
2. 2-о й с п о с о б
Проведем из угла АВС высоту ВК
ΔАВК - прямоугольный ( по построению)
sin∠ВАК² + cos∠ВАК² = 1 ---- по свойству тригонометрических функций угла
cos∠ВАК = √(1 - sin²∠ВАК) = √(1 - 0,28²) = √(1 - 0,0784) = √0,9216 = 0,96
cos∠ВАК = АК/АВ --- по определению
АК = АВ * cos∠ВАК = 25 * 0,96 = 24
Рассмотрим ΔВСК и ΔАВК. АВ = ВС -- по условию, ⇒ ∠ВАС = ∠ВСА - как углы при основании равнобедренного треугольника. ∠АВК = ∠СВК, - по свойству высоты равнобедренного треугольника ⇒ΔВСК =ΔАВ по стороне и двум прилежащим к ней углам ⇒ АК = СК = 24
АС = АК + СК = 24*2 = 48
Ответ: 48