Через вершину М равностороннего треугольника МРК проведен к его плоскости перпендикуляр...

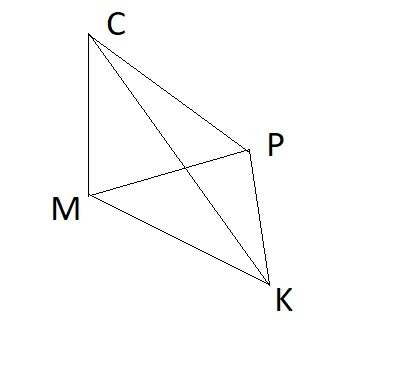
Т.к. CM ⊥ MPK, то проекцией прямой CK на плоскость MPK будет MK.

Т.е. ∠CKM = 60°, т.к. он и будет углом между прямой и плоскостью.

Тогда из прямоугольного ΔCMK найдем:

$MC=MK*tgCKM=PK*tgCKM=24*tg60=24\sqrt{3}$

ΔCPM = ΔCKM, т.к. они оба прямоугольные, у них общая сторона MC и MP = MK как стороны равностороннего треугольника.

Из равенства этих треугольников следует, что CP = CK

CK также найдем из прямоугольного ΔCMK

$CK=\frac{MK}{cosCKM}=\frac{24}{cos60}=48$