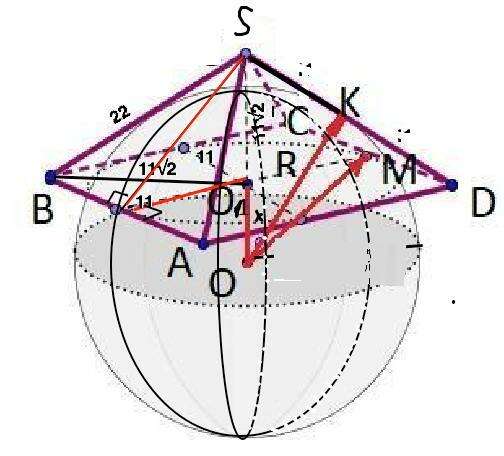
Радиус r окружности, вписанной в основание пирамиды, равен половине стороны квадрата.
O1M = r = 22/2 = 11.
Центр сферы находится на прямой, проходящей через высоту пирамиды (это для правильной пирамиды).
Составит систему уравнений из треугольников, включающих R к стороне основания, и к боковому ребру.
Это соответственно треугольники OKS и OMS.
Обозначим отрезок О1О = х.
Для пирамиды с равными рёбрами угол наклона бокового ребра к основанию равен 45 градусов. Отсюда вывод: треугольник OKS – прямоугольный равнобедренный.
KS = kO = R = (ОО1 + Н)/√2 = (х + Н)/√2.
Высота Н = L*sin 45° = 22*(√2/2) = 11√2.
Тогда R = (х + 11√2)/√2. (1)
Из прямоугольного треугольника МОО1 получаем R² = 11² + x². (2)
Возведём уравнение (1) в квадрат.
{R² = ((ОО1 + Н)/ √2)² = ((х + 11√2)/ √2)² = (х² + 22√2*х + 242)/2. (3)
Приравняем правые части уравнений (2) и (3).
(х² + 22√2*х + 242)/2 = 121 + х²,
х² + 22√2*х + 242 = 242 + 2х2.
Приведя подобные, получаем х² - 22√2*х = 0 или х(х - 22√2) = 0.
Имеем 2 корня: х = 0 и х = 22√2.
Второе значение даёт точку касания боковых рёбер на длине, равной радиусу R = 33 от вершины, то есть за пределами пирамиды. Это решение отбрасываем.
Ответ: R₁ = (0 + 11√2)/√2 = 11.